
브라질에서 나비 한 마리가 날개를 퍼덕이면 그 작은 효과가 연결된 여러 요인의 복잡한 상호작용을 거쳐서 저 멀리 텍사스에 커다란 토네이도를 만들어 낼 수도 있다. 바로 ‘나비 효과’라고 불리는 흥미로운 현상이다. 작은 나비 한 마리가 날개를 퍼덕이면 반드시 토네이도가 발생한다는 얘기가 아니다. 날개를 퍼덕였을 때와 아닐 때, 처음의 작은 차이에 의해 그 결과로 텍사스에 토네이도가 생길 수도 아닐 수도 있다. 둘 중 어떤 결과를 만들어낼지 브라질의 나비 한 마리를 유심히 관찰한다고 미리 알아내는 것은 불가능하다. 모든 나비를 움직이지 못하게 한다고 토네이도를 막을 수도 없다. 나비가 아니면 잠자리가, 잠자리가 아니면 파리 한 마리가 토네이도를 만들어 낼 수도 있다. 이처럼 처음 조건의 작은 차이가 결과에 큰 차이를 만들어낼 수 있어서 장시간 뒤의 미래를 예측할 수 없다는 것이 ‘카오스 현상’이고, 카오스 현상을 브라질 나비와 미국 토네이도로 비유한 것이 나비 효과다.
기상현상을 설명하는 수치 모형에서 에드워드 로렌츠(Edward Lorenz)가 1960년대에 발견한 카오스는 이후 여러 시스템에서도 연이어 확인된 바 있다. 수리 생물학자 로버트 메이(Robert May)는 1976년 출판한 논문에서 간단한 모형으로부터 아주 복잡한 동역학적 결과가 만들어진다는 것을 보였는데, 이때 메이가 이용한 방정식이 바로 ‘병참 본뜨기’(logistic map)다. 병참 본뜨기는 시간이 띄엄띄엄 변하는 모형이다. 토끼가 올해 9월 1일 몇 마리인지 세고, 내년 같은 날에 또 몇 마리인지 세는 과정을 이어간다고 생각해보자. 올해를 첫 번째(n=1)로 설정하면, 내년은 두 번째(n=2) 해가 된다. 일정한 넓이의 풀밭과 같은 제한된 서식 환경에서 살아갈 수 있는 최대 토끼 수를 생각할 수 있다. 토끼의 최대 개체 수를 기준으로 해서 토끼가 n번째 해에 몇 마리인지를 세고, 그 비율을 Xn으로 적으면 Xn은 토끼가 단 한 마리도 없을 때는 0의 값을, 그리고 환경이 허락한 최대 토끼 수에 도달할 때는 1의 값을 갖는 변수가 된다. 그리고 n+1번째 값 Xn+1은 바로 앞 n번째의 값 Xn으로부터 결정된다고 가정할 수 있다.
만약 토끼가 올해 최대 개체 수의 10%(=0.1)이고 매년 개체 수가 두 배로 늘어난다면 어떤 일이 생길까? 내년에는 20%, 그리고 그 이듬해에는 40%가 된다. 이처럼 매해 두 배씩 토끼 개체 수가 늘어난다면 이 상황을 설명하는 식은 Xn+1 = 2·Xn이다. 이 식에 X1 = 0.1을 넣으면, X2 = 0.2, X3 = 0.4가 된다는 것으로 쉽게 이해할 수 있다. 같은 계산을 두 번만 더 이어가면, X4 = 0.8, X5 = 1.6을 얻는데, 다섯 번째 해의 값 1.6은 환경이 최대로 허락한 토끼의 개체 수보다 더 많은 토끼가 있다는 뜻이다. 하지만, 토끼의 최대 개체 수가 정해져 있는 유한한 서식 환경이라면 Xn의 값은 1을 넘을 수 없다. 수식 Xn+1 = 2·Xn은 아무런 제한 없이 토끼가 무한대로 증식할 수 있을 때만 맞는 식이어서 서식 환경에 제한이 있을 수밖에 없는 실제 현실에 적용될 수 없다.
토끼의 개체 수가 점점 늘어나면 무슨 일이 생길까? 토끼 한 마리는 다른 토끼들과 풀밭의 풀을 놓고 서로 경쟁한다. 다른 토끼가 많다면 경쟁이 심해지고, 토끼가 늘어나는 경향이 약해지게 된다. 앞에서 적은 식 Xn+1 = 2·Xn에 토끼의 경쟁에 의한 효과를 넣으면 Xn+1 = 2·Xn·(1-Xn)의 꼴로 적을 수 있다. X1 = 0.1을 넣고 차례로 살펴보면 0,180, 0.295, 0.416, 0.486...의 수열을 따라 토끼가 늘어난다. 시간이 흐르면서 토끼의 증가세가 완만해지고, 아무리 시간이 지나도 Xn의 값은 환경이 허락한 최대치인 1.0을 넘을 수 없다는 것을 알 수 있다. 위의 식에서 토끼의 증가율 2를 매개변수 r로 일반화한 것이 메이가 1976년 논문에서 자세히 살펴본 병참 본뜨기 모형의 식 Xn+1 = r·Xn·(1-Xn)이다. 환경에 제약이 있는 상황에서 개체수 변화를 기술하는 단순한 식인데도, 이 간단한 이차식으로부터 얻어지는 결과는 정말 놀라울 정도로 복잡하다.
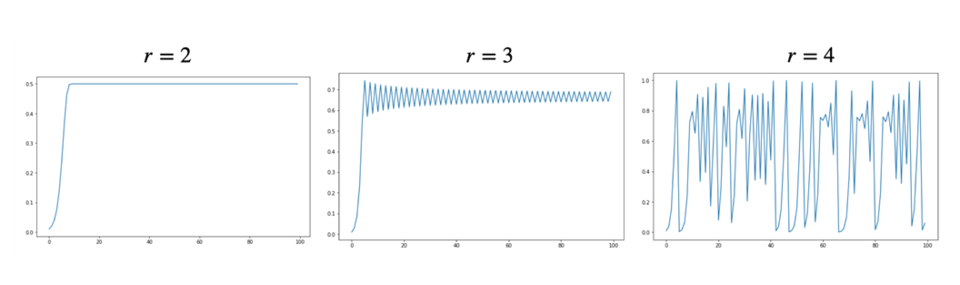
아래 그림은 각각 r = 2, 3, 4일 때, 처음 조건으로 X1 = 0.01을 이용해 그린 병참 본뜨기의결과다. r = 2일 때는 일정한 값으로 수렴하는 것을 볼 수 있고, r = 3일 때는 주기적으로 오르내리는 규칙적인 모습을 볼 수 있다. 이 경우 개체 수는 세대마다 두 값을 번갈아 가며 갖게 된다. 그림에서 가장 흥미로운 것이 r = 4의 경우다. 토끼가 도대체 몇 마리가 될지가 끊임없이 뒤죽박죽 변하고, 아무런 주기적인 거동을 볼 수 없다. 바로 카오스가 등장하는 영역이다. 정말 간단한 식으로부터 얻어지는 놀랍도록 복잡한 현상이다.
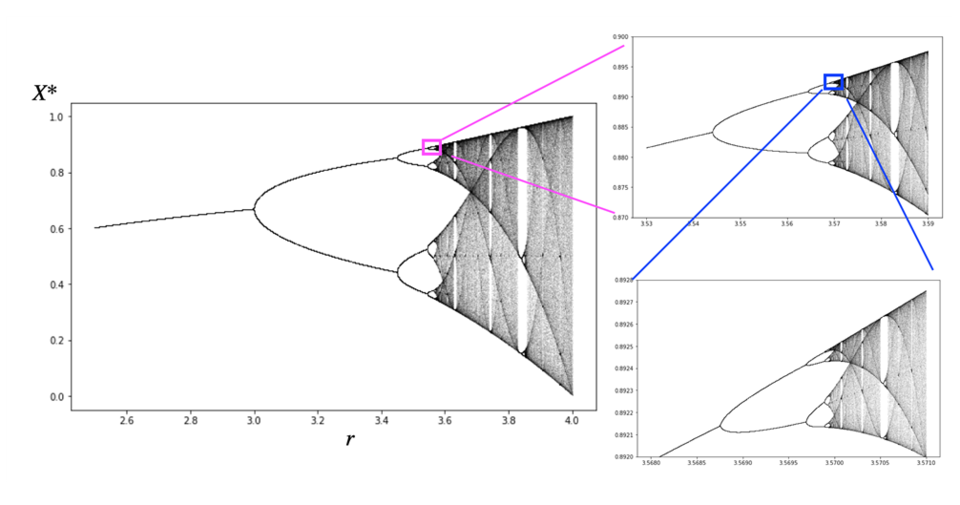
병참 본뜨기의 결과를 다른 방식으로 그래프로 그릴 수 있다. 토끼의 증가율 r을 변화시키면서 한참 세대가 지난 다음의 최대 허용 개체 수 대비 토끼 수인 Xn을 그래프로 표시하면 아래 그림을 얻게 된다. r이 점점 늘어나면 두 가지의 갈래로 분기하는 것을 볼 수 있고, 더 늘어나면 다음의 분기를 또 볼 수 있다. 이를 ‘쌍갈래질’(bifurcation)이라고 부른다. 쌍갈래질 그림을 보면 무척 흥미로운 모습이 보인다. 바로 부분을 확대하면 전체와 비슷한 모습이 끊임없이 반복되는 프랙털(쪽거리, fractal)이다.
20세기 중엽 여러 간단한 시스템에서 카오스를 볼 수 있다는 것이 널리 알려졌다. 처음 수식에서 발견된 카오스 현상을 실제 생태계에서의 개체 수 변화에서도 과연 관찰할 수 있을까? 연구자들이 당연히 관심을 가져야 할 중요한 질문이었다. 하지만, 실제 개체 수의 시간 변화 데이터를 이용한 그동안의 여러 연구에서 현실에서는 카오스를 볼 수 있는 경우가 그리 많지 않다는 것이 알려지게 된다. 과연 카오스는 복잡한 현실을 극히 단순화한 간단한 수식에서만 볼 수 있을 뿐인지, 아니면 현실에도 카오스가 숨어 있지만 과학자들이 아직 카오스를 제대로 보는 방법을 찾지 못한 것인지는 중요한 문제였다.
얼마 전 출판된 한 논문(DOI:10.1038/s41559-022-01787-y)의 저자들은 누구나 인터넷에서 내려받을 수 있는 여러 종의 개체 수 시간 변화 데이터를 치밀하게 살펴봤다. 카오스 현상을 발견하기 위해 이용하는 표준적인 방법 대신 여러 다른 수학적 방법을 현실의 개체 수 변화 데이터에 적용했다. 저자들의 방법 중 재미있던 것이 있다. 비선형 동역학 분야에서는 바로 앞 시간의 개체 수와 그 다음 시간의 개체 수 사이의 관계를 주로 살펴보는데, 논문의 저자들은 과거 N개 시점의 개체 수가 그 다음 시간에 영향을 줄 수 있는 방향으로 문제를 확장해서 카오스 여부를 판정했다. 기존의 연구들이 1차원 데이터를 가정한 것을 N차원 데이터로 확대해 살펴보는 방법이다.
논문 저자들은 170여 종의 개체 수 데이터를 자신들의 방법으로 분석해서 이 중 무려 33% 이상의 데이터에서 카오스를 발견했다. 현실 생태계에도 카오스가 곳곳에 숨어있었지만, 기존 연구자들의 카오스 분석 방법이 적절치 않았다는 주장인 셈이다. 카오스를 보이는 시스템은 시간이 지나면 미래를 예측하는 것이 어려워진다. 이때, 얼마나 오랜 시간이 흘러야 예측이 어려워지는지를 측정하는 양이 ‘랴푸노프 시간’(Lyapunov time)이다. 랴푸노프 시간이 개체의 평균 질량이 늘어나면 함께 늘어난다는 결과도 논문에 보고되었다. 몸이 더 큰 생명체의 경우 카오스를 보려면 더 오랜 기간의 개체 수 데이터가 축적되어야 한다는 의미다. 카오스는 이론뿐 아니라 현실 여기저기에도 숨어있지만, 주의 깊은 눈으로 볼 때 더 잘 보인다는 것이 논문의 결론이다. 현실에도 카오스가 흔하다. 흘깃 보지 말고 자세히 봐야 보인다.



